分类： 计算机组成原理

计组期末总结系列3——控制器

 

————————下面是一些开头的废话，可以不看————————

由于电脑坏了，又不能整天玩手机，舍友说计组不会，为了方便同学复习，同时总结一下整个学期学习的内容，所以决定写写一些重点的内容，另，本人水平有限，如果文中有错误还请批评指正。

——————我是分割线，上面的废话可以不看，下面才是重点———————

 

要说控制器，就要从头说起。当设计实现了运算器、存储器之后，再配合一些寄存器，就可以进行很多算数运算和逻辑运算了，无论是什么运算，在这门课中都是基于单总线结构来学习的。总线就是一排导线，我觉得把它叫做排线其实也没什么问题。这一排线的两端可以接不同的东西，一边输出数据、一边读入数据，就完成了两个设备之间的数据传递。

由于是单总线结构，所以只能同时一个设备输出数据。但是却可以多个设备同时输入数据。硬件上来说，总线的一端是根据需要连接不同的设备的。另一端连接着所有可以输入数据的设备，根据需要改变它们的片选信号即可控制哪个或者哪几个设备从总线读取内容。理解了这点，实验中无论多么复杂的操作也就可以理解了。其实实验那么多操作无非是干这几件事：更改总线的输入端设备、更改总线的输出端设备、进行一些运算。这几件事也是计算机能干的事情，输入、运算、输出。

下面的部分将从高层到底层逐层细化、分析原理，再从底层到高层逐层编码、简化操作。

对应不同的设备，这三个操作都不一样，对于每个设备自己来说都有不同的读入、输出、运算方法，体现了一种多态的特性，是不是非常像面向对象程序设计思想？？我们以面向对象的思想来说说不同设备的读入、运算、输出。这三个方法就叫做微指令。设备之间交换数据的媒介就是总线。

 

寄存器

读入：从总线读入数据到内部

运算：无

输出：内部数据输出到总线

 

ALU运算单元

读入：DR1从总线读入数据、DR2从总线读入数据

运算：选择运算方式

输出：运算结果输出到总线

 

其他设备类比都可以写出这套流程。把上面每个过程再细化为具体操作如下，其中每个操作叫做微操作控制信号，也可以叫做微命令。

 

寄存器

读入：LDxx = 1  YS = 11  KQD

运算：无

输出：RxxàBUS  YS = 00

 

ALU运算单元

读入：LDDR1 = 1  KQD、LDDR2 = 1  KQD

运算：S3 S2 S1 S0 M Cn = XXXXXX

输出：ALUàBUS = 1

 

如果所有设备都完成了上面的过程，那么每一个运算操作总能被划分为某设备的输入、运算、输出三种操作。这时候如果想做一个运算操作指令，只需要套用即可，举个例子来说：（R1）+（R2）à R1，步骤是这样的：

ALU读入

ALU运算

ALU输出

R1读入

套用上面的已经写好的流程

ALU读入

1. R1内容输出到总线
2. DDR1读入数据
3. R2内容输出到总线
4. DDR2读入数据

ALU运算

5. 选择运算方式

ALU输出

6. 运算结果输出到总线

R1读入

7. R1从总线读入数据

 

翻译为具体操作就是

 

1. R1àBUS = 1 YS = 00
2. LDDR1 = 1 KQD
3. R2àBUS = 1 YS = 00
4. LDDR2 = 1 KQD
5. S3S2S1S0 = 1001 M = 0  Cn = 0
6. ALUàBUS = 1
7. LDR1 = 1 YS = 11  KQD

————————这是分界线，接下来将逐层编码返回高层————————

 

你会发现，每次只有按完KQD才是完成了数据的传输，KQD之前的内容都是在更改总线输入端和输出端的设备及片选状态。当做了很多类似的操作时候，会发现很麻烦，这时候人们希望机器自动执行指定的操作。思想是这样的，设计一套指令格式，把这些内容存进一个存储器，需要执行的时候直接从这个存储器调用，这个存储器就叫做控制存储器。

既然都是更改状态+KQD，那么我们就可以把这些状态记下来，然后再执行KQD。这时候就会出现问题，怎么表示这些状态？这就是微指令编码的设计。

如果直接记录每个状态，也就是每一位记录一个片选信号状态，这种方法叫做直接控制法、也叫不译法。好处是执行速度很快，缺点是会导致整个状态记录后很长。

如果把所有的组合进行编码，就叫做全编码方法。每个编码对应一个微命令，那么编码长度会大大缩短，不过不好的是一段程序将有很多的微命令，会增加CM的访问次数，效率会下降。

如果综合前两种方式，那么就叫做字段编码表示法。把一些有冲突的操作进行编码，剩下的直接表示。那么执行的时候直接对编码过的字段线进行译码即可，剩下的线直接接到对应的片选管脚。

那么怎么告诉机器你想执行什么操作呢？机器听不懂人话，至少实验的那个机器听不懂，那么最好的办法就是再这个层次继续编码，每个编码对应连续的几个微指令（注意和微命令区分），这个编码的集合就叫做指令集。指令集的设计请自行查看课本（如果你明白了这个层次，那么一定能明白课本课程的层次顺序和你做实验的层次顺序。其实课本是从上层向底层讲的，而实验是从底层向上做的，正好相反。）

这些指令存在一个独立的寄存器中，这个寄存器就是IR，指令寄存器。每次从指令寄存器取指令，译码后（第一层译码）执行对应由微程序构成的一段程序、微程序又由微指令构成，微指令再进行译码（第二层译码）产生微指令（微操作控制信号），这样就成了书中的那个层次图。在时钟脉冲的控制下，这个过程一直持续下去直到程序结束。这两层译码的部分再加上程序计数器、IR、时序发生器组合在一起，控制着整个流程的运转，所以叫做控制器。

计组期末总结系列2——存储器

 

————————下面是一些开头的废话，可以不看————————

由于电脑坏了，又不能整天玩手机，舍友说计组不会，为了方便同学复习，同时总结一下整个学期学习的内容，所以决定写写一些重点的内容，另，本人水平有限，如果文中有错误还请批评指正。

——————我是分割线，上面的废话可以不看，下面才是重点———————

 

在计算机中用于记录数据的硬件，就可以叫做存储器，比如内存。存储器以存储芯片为核心构成。关于存储芯片的原理我也说不清楚（电路学的不好-_-||）但是只需要知道它能保持电信号并且在需要的时候可以读出就行了。

在存储芯片内部，存储芯片排成一个矩阵，只需要给出相应的地址，就能读写制定的单元。每个单元可以存n位二进制数，一般是8位，正好是一个字节。顺便说一下单位的转换。

1个二进制位叫做1个比特，写作1bit（注意是小写）

8个二进制位叫做1个字节，写作1Byte（简写为1B，注意这是大写）

1024个字节叫做1千字节，写作1KB

1024个千字节叫做1兆字节，写作1MB

以此类推GB、TB等。。。

所以通常运营商所说的10M网的意思是10Mbps，也就是Mb/s，代表兆比特每秒而不是兆字节每秒。转换的话要除以8才是理论的下载峰值。

 

接着说存储单元地址，既然是矩阵，那么直接给出行列下标即可。为了说明原理，在不失去规律的前提下缩小规模，例如储存矩阵是4*4的，那么共有16个存储单元如图所示。

比如我要选择第2行第3列的位置，那么行号就是2，列号就是3，也就是2,3，但是每次给两个值太麻烦了，想办法转换成给一个数字，并且希望数字加1后自动换行，比如2,3的下一个就是30。最好的办法就是用四进制的数字23代表地址，23+1 结果正好是30。同时为了电路实现方便，采用2进制来表示，并且可以直接用3-8译码器之类的芯片来选择不同的行和列。具体电路就是分别把前两位和后两位送入两个译码器即可。

比如上面的地址就可以写成1011，前两位是行下标，后两位是列下标。这不是巧合，还记得上次说过二进制、八进制、十六进制的转换吧，四进制也同理，每两位二进制数位正好是是一位四进制数位的权值。这样上图这16块地址单元就可以通过4位的二进制数字来表示了，也就是地址长度为4位。如果给定存储器大小计算地址长度，则直接看这个数2的几次幂即可。

 

扩展位数和扩展容量

如果用一个存储芯片直接作为一个存储单元的话，可能会出现位数不够的情况，比如一片存储芯片只能存4bit，但是需要做成每个单元存8bit的存储矩阵。那么就需要同时用两片芯片来共同工作，一个存前（高）四位一个存后（低）四位，首先要先理解工作原理才能理解接线的方法。一个芯片的原理图如下

以上文中的RAM为例，只是示意图，为了说原理，实际并没有这么小的芯片。其中A的引脚是地址引脚，CS是片选、WE是读写功能选择。D引脚是数据引脚，可读可写。

想要扩展每个单元的位宽，也就是说当选择一个单元的时候，两片芯片选择的地址应该相同，并且要同时生效、功能一样。所以，地址引脚、片选、读写选择都应该接到一起。如下图

由于需要一个存储高4位一个存储低4位，所以地址线要分别接起来。如图

第二个芯片的四位正好充当了高四位的储存。

 

还有一种情况，假如位数够了容量不够怎么办？同理，想要多大的容量就用多少芯片组合工作，还是先说原理，当一个芯片不够的时候，我们需要多个芯片同时储存不同的信息，也就是说用下一个芯片的第一个地址单元当上一个芯片最后一个单元的下一个单元，比如上文中最大地址号是1111那么下一块本来已经没有了，因为四位最大就是1111，但是我们希望储存到下一个芯片的第0个地址，0000，同时还要满足地址的连续，而1111+1 = 10000，后四位正好是0000，那么你一定发现了，第4位也就是D4(从左到右依次为D4D3D2D1D0)代表了第几块芯片。

另外，当地址为10000的时候还要保证第二块芯片生效而第一块无效，所以片选这时候就要单独考虑了，存储芯片的片选是低电平有效，所以直接用一个非门即可（三片以上用译码器），由于控制了片选，所以读写接到一起是没问题的，并且数据线也同理接到一起。

另外的一种接法就是这两种的综合，同时扩展位宽和容量。思路是这样的，先扩展位宽，之后把扩展位宽后的两片当做一个整体，再扩展容量。接线图如下。

接下来说说cache，为了提高CPU从存储器读取数据的速度，所以设计了缓存，思路是这样的，短期内读取过的数据做一个临时的存储，再次读到的时候不再访问主存，直接读缓存。举个例子，比如我让你算1234+567，你可能要算下，结果是1801，如果我只过两秒问你同样的问题，那么第二次你的回答就会直接是你刚刚计算过的结果，并且短时间内问你同样的问题你都不会再去计算。这就是缓存。（扯点题外话，在大型网站的开发中会大量利用缓存基础来提高效率或者分流访问流量。）

缓存通常容量很小，但是读取速度很快。做缓存的方法有这么几种，直接映像、全相联映像、组相联映像。本文依然在不丢失规律的前提下缩小规模，便于观察原理。仅以直接映像为例进行说明，其他的类似。

假设主存有32字节、缓存有16字节（实际上主存会远大于缓存）如左下图，所以主存地址5位就够了，在表中用十六进制表示

我们的目的是要用16字节的内容来记录32字节中的部分内容，首先以4字节为单位划分缓存和主存，如上右图，主存会分成8块，缓存会分成4块。再按照缓存的大小继续划分主存，可以得到2个区，直接映像的思路是直接用缓存中对应的块来对应映射主存中的块。

缓存中第0块只对应主存中的第0区第0块或者第1区第0块（也就是第4块）。

缓存中第1块只对应主存中的第0区第1块或者第1区第1块（也就是第5块）。

缓存中第2块只对应主存中的第0区第2块或者第1区第2块（也就是第6块）。

缓存中第3块只对应主存中的第0区第3块或者第1区第3块（也就是第7块）。

那么问题来了，怎么区分缓存中存的内容是主存中的第几个区的内容？

需要一个表来记录，由于位置相对不变，只是不知道对应主存中的第几个区，所以只记录区号即可，这个表就叫做块表。缓存被划分了多少块表就有多少行，每行里的内容存储的就是这块缓存对应了主存中的哪个区。

举个例子来看，以1C号内存为例，内存地址是0001 1101（A7A6A5A4A3A2A1），按照划分规则，则A1A0代表的就是块内地址，A3A2代表的就是区内块号、剩下的1位就是区号。如果你这些都明白了，再去仔细看下课本，一定会很轻松。

计组期末总结系列1——数的表示

 

————————下面是一些开头的废话，可以不看————————

由于电脑坏了，又不能整天玩手机，舍友说计组不会，为了方便同学复习，同时总结一下整个学期学习的内容，所以决定写写一些重点的内容（虽然导论、C语言、电路都讲过三遍了，然而还是可以有人不会啊╮(╯▽╰)╭）。另，本人水平有限，如果文中有错误还请批评指正。

——————我是分割线，上面的废话可以不看，下面才是重点————————

在计算机中，所有的数字都是用二进制来表示的，为了理解记忆而不去记忆大量的公式，不得不从头好好思考二进制。

我们都知道在十进制中，以一个数字为例：1234.4321，想想这个数字的含义，如果什么都不说，我们都会默认这是一个十进制的数字。1234.4321 = 1234 +0.4321，可以分成两个部分来表示，也就是整数部分和小数部分。我们分别来看这两个部分。

1234     = 1 * 1000 + 2 * 100 + 3 * 10 + 4 * 1

= 1 * 10^3 + 2 * 10^2 + 3 * 10^1 + 4 * 10^0

每一位代表着不同的意义，从右往左看

第0位的数字代表了有多少个1，也就是10^0

第1位的数字代表了有多少个10，也就是10^1

第2位的数字代表了有多少个100，也就是10^2

第3位的数字代表了有多少个1000，也就是10^3

以此类推

0.4321 = 4 * 0.1 + 3 * 0.01 + 2 * 0.001 + 1 * 0.0001

= 4 * 10^-1 + 3 * 10^-2 + 2 * 10^-3 + 1 * 10^-4

小数点后的部分，从左往右看

第0位的数字代表了有多少个0.1，也就是10^-1

第1位的数字代表了有多少个0.01，也就是10^-2

第2位的数字代表了有多少个0.001，也就是10^-3

第3位的数字代表了有多少个0.0001，也就是10^-4

上面所说的十进制代表了每位数字的权值都是10的幂次。

同理类推到二进制。

 

以1010.1001为例

1010.1001 = 1010 + 0.1001

整数部分，从右往左看

1010      = 1 * 8 + 0 * 4 + 1 * 2 + 0 * 1

= 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 0 * 2^0

 

第0位的数字代表了有多少个1，也就是2^0

第1位的数字代表了有多少个2，也就是2^1

第2位的数字代表了有多少个4，也就是2^2

第3位的数字代表了有多少个8，也就是2^3

 

小数点后的部分，从左往右看

0.1001 = 0.1 + 0.00 + 0.000 + 0.0001

=1 * 2^-1 + 0 * 2^-2 + 0 * 2^-3 + 1 * 2^-4

第0位的数字代表了有多少个0.5，也就是2^-1

第1位的数字代表了有多少个0.25，也就是2^-2

第2位的数字代表了有多少个0.125，也就是2^-3

第3位的数字代表了有多少个0.0625，也就是2^-4

八进制和十六进制同理。

 

进制之间的转换：

十进制  二进制  八进制  十六进制

如果你理解了上面所述的含义，那么转换也会非常容易理解。不同进制数字的含义最终都是为了表示数字，换句话说也就是一个数字可以以不同的方式表示出来。

 

十进制转二进制方法

以1234.4321为例进行说明。

整数部分的转换：

由于二进制每位的权值都是2的幂次，所以为了方便转化可以先写出几个算好的2幂次结果

2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
1024	512	256	128	64	32	16	8	4	2	1

 

寻找小于1234且尽可能大的数或者等于1234的位写1，如下表

 

2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
1024	512	256	128	64	32	16	8	4	2	1
1

用1234 – 1024 = 210

寻找小于210且尽可能大的数或者等于210的位继续写1，如下表

 

2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
1024	512	256	128	64	32	16	8	4	2	1
1			1

 

用210 – 128 = 82

寻找小于82且尽可能大的数或者等于82的位继续写1，如下表

 

2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
1024	512	256	128	64	32	16	8	4	2	1
1			1	1

 

用82 – 64 = 18

寻找小于18且尽可能大的数或者等于18的位继续写1，如下表

 

2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
1024	512	256	128	64	32	16	8	4	2	1
1			1	1		1

 

用18 – 16 = 2

寻找小于2且尽可能大的数或者等于2的位继续写1，如下表

 

2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
1024	512	256	128	64	32	16	8	4	2	1
1			1	1		1			1

 

最后，剩余位写0，结果就是转换成二进制的整数部分。

 

2^10	2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0
1024	512	256	128	64	32	16	8	4	2	1
1	0	0	1	1	0	1	0	0	1	0

 

结果为 10011010010

 

小数部分0.4321，进行乘二取整。

0.4321 * 2 = 0.8642  整数部分为0

0.8642 * 2 = 1.7284  整数部分为1

0.7284 * 2 = 1.4568  整数部分为1

0.4568 * 2 = 0.9136  整数部分为0

0.9136 * 2 = 1.8272  整数部分为1

以此类推直到小数部分为零，把上面取到的整数部分从左到右排列即是二进制小数0.01101，注意，需要几位就算几次。

 

其他的转换：

二进制，八进制，十六进制之间都可以方便的进行转换，因为每三位二进制数字相当于八进制的一位数字，每四位相当于十六进制的一位数字。

 

定点整数的表示

首先，在计算机中所有的数字都是二进制储存的，但是，为了方便书写和节省位数一般用十六进制来表示，两位就能表示八位的二进制数字。

编码有三种，原码，反码，补码。接下来详细说明。为了方便观察，我们在能观察规律的情况下尽可能缩短长度来说明。

由于有正数和负数，所以需要一位标识位来区分是正数还是负数。先说原码，取字长位三位，其中第一位是符号位，0代表正1代表负，那么它可以表示的数字是这样的、

	原码			真值
0	0	0	0	0
1	0	0	1	1
2	0	1	0	2
3	0	1	1	3
4	1	0	0	-0
5	1	0	1	-1
6	1	1	0	-2
7	1	1	1	-3

 

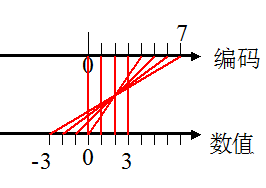
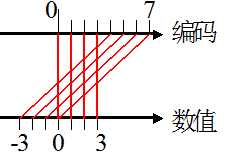
表中第一列是单纯作为二进制来看这三位数的十进制数字。原码的特点非常容易看出来，有两个0，一个是100一个是000，都是代表了0，表达的范围是对称的。计算方法也很好理解，由于只有2位可以用来表示数本身，所以可以表示的数范围就是0 ~(2^2)-1也就是0~3，算上负数的那部分也就是-3~+3，推广一下很容易得到范围的公式，-((2^n)-1)~+(2^n)-1，也就是1-2^n~2^n-1，其中的n是不算符号位在内的位数。

最大的正数是011，也就是3，

最小的正数是001，也就是1

最大的负数（绝对值最小的负数）是101，也就是-1

最小的负数（绝对值最大的负数）是111，也就是-3

 

接下来是反码，需要注意的是，正数的反码和原码一样，正数的反码和原码一样，正数的反码和原码一样，负数的反码就是把原码按位取反得到的，符号位不变。符号位不变。符号位不变。（重要的事情说三遍）效果如下表

	反码			真值
0	0	0	0	0
1	0	0	1	1
2	0	1	0	2
3	0	1	1	3
7	1	1	1	-0
6	1	1	0	-1
5	1	0	1	-2
4	1	0	0	-3

 

显然，范围没变，但是对应关系有了一些变化，和原码表示相同的是，0依然有可以有2个编码来表示。

最后是补码，正数的补码和原码一样。正数的补码和原码一样。正数的补码和原码一样。负数的补码是在它的反码基础上再加1，这个加1的运算符号位要参与运算。这个加1的运算符号位要参与运算。这个加1的运算符号位要参与运算。效果如下。

	补码			真值
0	0	0	0	0
1	0	0	1	1
2	0	1	0	2
3	0	1	1	3
0	0	0	0	0
7	1	1	1	-1
6	1	1	0	-2
5	1	0	1	-3

结果会发现还有一个编码空着，就是100，所以规定用100表示-4，如下表

	补码			真值
0	0	0	0	0
1	0	0	1	1
2	0	1	0	2
3	0	1	1	3
0	0	0	0	0
7	1	1	1	-1
6	1	1	0	-2
5	1	0	1	-3
4	1	0	0	-4

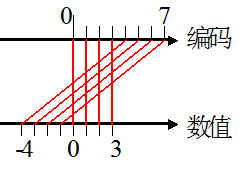
这样既可以多表示一个数字，扩大了表示范围，还统一了0的编码。并且用补码表示还有一个特点，仔细观察上面的表格，如果用111+001，结果将会是000，高位会直接溢出而消失。正好和-1+1 = 0吻合。所以计算机中都用二进制补码来表示数字。补码能表示的范围显然是-(2^2)~2^2-1，推广下就是-(2^n)~2^n-1，其中的n依然不包括符号位在内。

最大的正数是011，也就是3，

最小的正数是001，也就是1，

最大的负数（绝对值最小的负数）是111，也就是-1，到此为止和原码一样

最小的负数（绝对值最大的负数）是100，也就是-4，

注意：这个数字很特殊，真值不能直接求原码来算。可以由以下两种思路来理解。

第一种：按照原码中最小的负数再减1来计算。比如

三位的编码最小的负数用原码表示为111，是-3，那么这个数就代表的是-4

四位编码中最小的负数用原码表示为1111，是-7，那么1000就代表-8

第二种：按照一对儿相反数相加为0来考虑。

寻找一个和100相加为000的数，那么是一定是100，把这个100当成二进制编码来换成十进制，也就是4，那么补码100代表的就是-4

简化过程就可以直接把补码100当成二进制转换，结果再取反即可得到补码100的真值。

再比如补码1000，转成十进制就是8，那么它表示的真值就是8的相反数-8

 

注意总结上面的规律（前提条件是以补码表示）

最大的正数：

符号位一定是0，由于要求是最大，所以剩下的位数都是1即可，以8位编码为例，最大的正数就是0111 1111。可以按权值展开计算真值，但是这里有个小技巧，可以先把这个数加1,结果是1000 0000，然后转换，结果是2^7 = 128，之后再减1，也就是127。所以考试如果出现n位的话可以直接写出结果，也就是2^(n-1)-1。

最小的正数就不用说了，一定是1。

最大的负数（绝对值最小的负数）：

有几位就写几位1，以8位编码举例，就写8个1，也就是 1111 1111，真值以上面第二种思路来理解非常方便，结果是-1.

最小的负数（绝对值最大的负数）：

符号位一定是1，剩下几位写几个0。以8位编码为例，就写1000 0000，真值类比上面的思路来求，结果是-128。

这几个数在数轴上的位置如下图

接下来说说定点小数的表示。

在十进制中，表示的方法都很熟悉了，但是一定要仔细思考含义，才能理解二进制中定点小数的表示。

十进制中：把1个1分成10份，其中的一份就表示为0.1，如果分成100份，其中的一份就是0.01，如果分成1000份，其中的一份就是0.001

二进制中同理，把1个1分成2份，其中的一份就表示为0.1，如果分成4份，其中的一份就是0.01，如果分成8份，其中的一份就是0.001

注意虽然写出来一样，但是含义完全变了。

由于是小数，所以整数部分是0，延续定点整数的思路，把这位数当做符号标识，称为符号位。类比前面整数部分，依然可以有如下的三种表示方法，按顺序分别是原码，反码，补码。依然以3位编码为例。

	原码			真值
0	0	0	0	0.00	0.00
1	0	0	1	0.25	2^-2
2	0	1	0	0.50	2^-1
3	0	1	1	0.75	(2^-1)+(2^-2)
4	1	0	0	-0.00	-0.00
5	1	0	1	-0.25	-2^-2
6	1	1	0	-0.50	-2^-1
7	1	1	1	-0.75	-((2^-1)+(2^-2))

最大的正数是011，也就是0.75，

最小的正数是001，也就是0.25，

最大的负数（绝对值最小的负数）是101，也就是-0.25，

最小的负数（绝对值最大的负数）是111，也就是-0.75，

	反码			真值
0	0	0	0	0.00	0.00
1	0	0	1	0.25	2^-2
2	0	1	0	0.50	2^-1
3	0	1	1	0.75	(2^-1)+(2^-2)
7	1	1	1	-0.00	-0.00
6	1	1	0	-0.25	-2^-2
5	1	0	1	-0.50	-2^-1
4	1	0	0	-0.75	-((2^-1)+(2^-2))

 

	补码			真值
0	0	0	0	0.00	0.00
1	0	0	1	0.25	2^-2
2	0	1	0	0.50	2^-1
3	0	1	1	0.75	(2^-1)+(2^-2)
0	0	0	0	-0.00	-0.00
7	1	1	1	-0.25	-2^-2
6	1	1	0	-0.50	-2^-1
5	1	0	1	-0.75	-((2^-1)+(2^-2))

同理，补码空余出了一个编码就是100，所以规定用100来表示-1、用100来表示-1、用100来表示-1

	补码			真值
0	0	0	0	0.00	0.00
1	0	0	1	0.25	2^-2
2	0	1	0	0.50	2^-1
3	0	1	1	0.75	(2^-1)+(2^-2)
0	0	0	0	-0.00	-0.00
7	1	1	1	-0.25	-2^-2
6	1	1	0	-0.50	-2^-1
5	1	0	1	-0.75	-((2^-1)+(2^-2))
4	1	0	0	-1

 

最大的正数是011，也就是0.75，

最小的正数是001，也就是0.25，

最大的负数（绝对值最小的负数）是111，也就是-0.25，到此为止和原码一样

最小的负数（绝对值最大的负数）是100，也就是-1，

注意：这个数字很特殊，真值不能直接求原码来算。

 

注意总结上面的规律（前提条件是以补码表示）

最大的正数：

符号位一定是0，由于要求是最大，所以剩下的位数都是1即可，以8位编码为例，最大的正数就是0111 1111。可以按权值展开计算真值，但是这里有个小技巧，可以先把这个数加0000 0001,结果是1000 0000，然后转换，结果是1，之后再减0000 0001，也就是1-2^-7。所以考试如果出现n位的话可以直接写出结果，也就是1-2^-n。其中的n不算符号位

最小的正数：

符号位一定是0，由于要求最小，所以把权值最小的最低位直接写1，以8位编码为例，结果是0000 0001，表示2^-7

最大的负数（绝对值最小的负数）：

符号位一定是1，剩下几位写几个1。以8位编码为例，就写1111 1111，真值类比上面的思路来求，结果是-(1-2^-7)。

最小的负数（绝对值最大的负数）：

符号位一定是1，剩下几位就写几个0，以8位编码为例，就是1000 0000，那么它一定是-1。

 

画张图更好理解这四个数字的位置。

最后是浮点数。

把定点整数和定点小数结合起来表示，就是浮点数。它的原理类似于科学计数法，比如1.5*10^50，那么只需要把1.5和50记下来，就能描述一个非常大的数字，同理也可以描述非常小的数字，指数部分就相当于记录了小数点的位置。所以仿照这个方法，也可以把一个数表示成0.8*2^30的形式，再记录下0.8和30两个部分来表示这个很大的数字，这就是浮点数的表示法。前面的部分称之为尾码，指数部分称之为阶码。尾码部分用上面的定点小数来表示，指数部分用定点整数来表示。阶码在前尾码在后，组合后的编码就是浮点数的编码。

浮点数的表示范围由于受尾码影响，所以和定点小数范围类似，但是又因为阶码的存在扩大了范围，所以在非常接近0的部分是无法表示的。可以看出，尾码的正负决定了整个浮点数的正负，阶码的大小决定了与0的距离。仔细思考这句话，你就能准确的找到浮点数的表示范围。要时刻记得阶码当成定点整数尾码当成定点小数。

下面以8位浮点数编码为例，规定前4位为阶码，1位符号位，后4位为尾码，1位符号位。均以补码表示

 

最大的正数：

 

要求阶码是最大的正数，

同时尾码也是最大的正数。

结果是0111 0111，

前4位当成定点整数求真值，为2^3-1 = 7

后4位当成定点小数求真值，为1-2^-3 = 0.875(注：如果幂次太高可以不算结果)，

所以最终表示的真值是0.875*2^7

 

 

 

最小的正数：

 

要求阶码为最小的负数（绝对值最大负数），

同时尾码为最小的正数。

结果是1000 0001，

前4位当成定点整数求真值，为-2^3 = -8

后4位当成定点小数求真值，为2^-3 = 0.125，

所以最终表示的真值是0.125*2^-8

 

 

 

最大的负数（绝对值最小的负数）：

 

要求阶码为最小的负数（绝对值最大负数），

同时尾码为最大的负数（绝对值最小负数）。

结果是1000 1111，

前4位当成定点整数求真值，为-2^3 = -8

后4位当成定点小数求真值，为-2^-3 =-0.125，

所以最终表示的真值是-0.125*2^-8

 

 

 

最小的负数（绝对值最大的负数）：

 

要求阶码为最大的正数，

同时尾码为最小的负数（绝对值最大负数）。

结果是0111 1000，

前4位当成定点整数求真值，为2^3-1 = 7

后4位当成定点小数求真值，为-1，所以最终表示的真值是-1*2^7

 

综上所述，浮点数的范围为-1*2^7~-0.125*2^-8  0.125*2^-8~0.875*2^7

 

但是为了提高运算精度，所以做了规格化（证明略），受影响的就是接近0左右两边的两个分界点。规格化后变化如下

最大负数（绝对值最小负数）变为1000 1011尾码变成了-((2^-1)-(2^-3)) = -0.375，结果是-0.375*2^-8

最小正数变为1000 0100 尾码变成了2^-1 = 0.5，结果是0.5*2^-8

所以规格后的范围是-1*2^7~-0.375*2^-8  0.5*2^-8~0.875*2^7